4. Организация и проведение диссертационного исследования

4.5. Корректность математической обработки результатов эксперимента – залог достоверности научных положений по диссертации

Эксперимент является важнейшим средством получения новых знаний не только в области естественных и технических наук, но и в экономике, социологии, политике, психологии, литературоведении и в других отраслях. Экспериментальные исследования дают критерии оценки обоснованности и приемлемости на практике любых теорий и теоретических предположений. Одним из основных этапов любого эксперимента является статистическая обработка экспериментальных данных. Она направлена, как правило, на построение математической модели исследуемого объекта или явления, а также на получение ответа на вопрос: «Достоверны ли полученные опытные данные в пределах требуемой точности или допусков?».

Сама же математическая модель в зависимости от целей эксперимента (исследование, управление, контроль) может быть использована для разных целей: для предметно-смыслового анализа объекта или явления, прогнозирования их состояния в разных условиях функционирования, управления ими в конкретных ситуациях, оптимизации отдельных параметров, а также для решения каких-то других специфичных задач. Особенно важна тщательная математическая обработка результатов экспериментов, подтверждающая теоретические выводы и построения по диссертациям на соискание ученых степеней.

Анализ результатов работы советов по защите диссертаций, а также экспертных советов ВАК Беларуси за последнее время свидетельствует о том, что для обработки экспериментальных данных не всегда выбираются методически обоснованные приемы, да и степень владения соискателями методиками такой обработки результатов экспериментальных исследований оставляет желать лучшего. Эксперты и оппоненты по диссертациям отмечают негативную тенденцию к снижению уровня подготовленности соискателей в понимании того, что они делают с помощью современной компьютерной техники при обработке опытных данных. Аспиранты БелНИИМЭСХ и БСХА 70-х годов прошлого столетия хорошо помнят крылатое выражение академика С.И.Назарова: «Если «дурь» заложишь в методику планирования эксперимента, а также в методику обработки его результатов, то «дурь» и получишь в итоге в выводах!». Это сегодня крайне актуально, так как никакой современной компьютерной техникой нельзя прикрыть изъяны вузовской и аспирантской подготовки.

Применение статистических методов обработки экспериментальных данных, критериев достоверности и адекватности моделей изучаемым процессам или явлениям, оценка точности и надежности результатов эксперимента требует знания основных положений теории вероятностей и математической статистики, умелого использования принципов и приемов программирования. Кроме того, в связи с усложнением алгоритмов обработки данных необходимы глубокие знания основных вычислительных методов. Статистические методы, методы вычислительной математики и программирование в вузах традиционно изучаются раздельно, однако только при комплексном использовании полученных из этих курсов знаний можно достигнуть успеха. Анализ учебных планов подготовки студентов по разным специальностям свидетельствует о постоянном увеличении числа изучаемых предметов. Это ведет к уменьшению числа учебных часов, выделяемых на общеобразовательные дисциплины, в том числе и математическую подготовку. С сожалением приходится констатировать факт все более усиливающейся прагматичности обучения, т.е. все дальше мы удаляемся от основополагающего принципа советской высшей школы по фундаментальности образования. В этих условиях в учебных и научных учреждениях и организациях, имеющих аспирантуру и докторантуру, необходимо введение специальных курсов по обучению особенностям применения математических методов для планирования эксперимента, сбора информации в виде экспериментальных данных по исследуемому объекту или явлению, а также по их последующей обработке с обеспечением требований надежности и точности. В качестве положительного примера организации таких курсов можно привести БГАТУ, в котором академиком И.С.Нагорским будущим научным сотрудникам и конструкторам сельскохозяйственной техники читается подобный курс, включающий практические решения задач по различным вопросам.

Конечной целью любой обработки экспериментальных данных является выдвижение гипотез о классе и структуре математической модели исследуемого явления, определение состава и объема дополнительных измерений, выбор возможных методов последующей статистической обработки и анализ выполнения основных предпосылок, лежащих в их основе. Для ее достижения необходимо решить некоторые частные задачи, среди которых можно выделить следующие:

1. Анализ, выбраковка и восстановление аномальных (сбитых) или пропущенных измерений. Эта задача связана с тем, что исходная экспериментальная информация обычно неоднородна по качеству. В основной массе результатов прямых измерений, получаемых с возможно малыми погрешностями, в экспериментальных данных часто имеются грубые ошибки, вызванные разными причинами. К ним могут быть отнесены просчеты экспериментатора, сбои вычислительной техники, аномалии в работе измерительных приборов и т. д. Без глубокого анализа качества данных, устранения или хотя бы существенного уменьшения влияния аномальных данных на результаты последующей обработки можно сделать ложные выводы об изучаемом объекте или явлении.

2. Экспериментальная проверка законов распределения экспериментальных данных, оценка параметров и числовых характеристик наблюдаемых случайных величин или процессов. Выбор методов последующей обработки, направленной на построение и проверку адекватности математической модели исследуемому явлению, существенно зависит от закона распределения наблюдаемых величин. При использовании для обработки процедур классического регрессионного анализа, в первую очередь, необходимо дать ответ на вопрос: «Является ли закон распределения наблюдаемых величин гауссовским и некоррелированным?» Получаемые при решении этой задачи выводы о природе экспериментальных данных могут быть как общими (независимость измерений, их равноточность, характер погрешностей и др.), так и содержать детальную информацию о статистических свойствах данных (вид закона распределения, его параметры). Решение центральной задачи предварительной обработки не является чисто математическим, а требует также и содержательного анализа изучаемого процесса, схемы и методики проведения эксперимента.

3. Группировка исходной информации при большом объеме экспериментальных данных. При этом должны быть учтены особенности их законов распределения, которые выявлены на предыдущем этапе обработки.

4. Объединение нескольких групп измерений, полученных, возможно, в различное время или в различных условиях, для совместной обработки.

5. Выявление статистических связей и взаимовлияния различных измеряемых факторов и результирующих переменных, последовательных измерений одних и тех же величин. Решение этой задачи позволяет отобрать те, переменные, которые оказывают наиболее сильное влияние на результирующий признак. Выделенные факторы используются для дальнейшей обработки, в частности, методами регрессионного анализа. Анализ корреляционных связей делает возможным выдвижение гипотез о структуре взаимосвязи переменных и, в конечном итоге, о структуре модели объекта исследований.

В ходе предварительной обработки, кроме указанных выше задач, часто решают и другие, имеющие частный характер: отображение, преобразование и унификацию типа наблюдений, визуализацию многомерных данных и др.

Следует отметить, что в зависимости от конечных целей исследования, сложности изучаемого явления и уровня априорной информации о нем объем задач, выполняемых в ходе предварительной обработки, может существенно изменяться. То же самое можно сказать и о соотношении целей и задач, которые решаются при предварительной обработке и на последующих этапах статистического анализа, направленных на построение модели явления. Так, например, если целью эксперимента является изменение значения неизвестной, но заведомо постоянной величины путем прямых многократных измерений с помощью средства измерений с известными характеристиками погрешностей, то полная обработка результатов измерения ограничивается простейшей предварительной обработкой данных (оценкой математического ожидания). В то же время, если измеряемая величина является переменной, а закон распределения погрешностей измерительного прибора неизвестен, то для решения конечной задачи потребуется проведение, как предварительной обработки данных, так и применение статистических методов исследования физических зависимостей.

Для решения задач предварительной обработки используются различные статистические методы: проверка гипотез, оценивание параметров и числовых характеристик случайных величин и процессов, корреляционный и дисперсионный анализ. Для предварительной обработки, оказывающей, как следует из сказанного, первостепенное влияние на качество решения конечных задач исследования, характерно итерационное решение основных задач, когда повторно возвращаются к решению той или иной задачи после получения результатов на последующем этапе обработки.

При обработке числовых массивов результатов эксперимента, как случайных величин, на практике применяют следующие выборочные оценки [9]:

• математическое ожидание

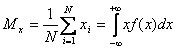
; ( 1 )

• дисперсия

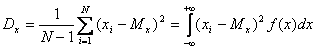
; ( 2 )

• коэффициент асимметрии

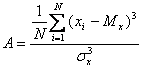
 ( 3 )

• коэффициент эксцесса

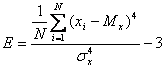
 ( 4 )

где 

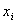
— значение результата в i-ом опыте;

N — число результатов в массиве;

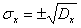
 — среднеквадратичное отклонение.

Производная оценка от величины математического ожидания и дисперсии является коэффициент вариации, определяемый в процентах по формуле [40]:

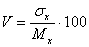
 ( 5 )

Дисперсия, среднее квадратичное отклонение и коэффициент вариации являются количественными характеристиками оценки рассеивания значений результатов эксперимента как случайной величины и применяются при изучении различных действий со случайным исходом. Коэффициент асимметрии и коэффициент эксцесса являются характеристиками более высшего порядка. Первый характеризует «скошенность распределения», а второй – степень его «островершинности» [104].

Вычисленные по экспериментально наблюдаемым случайным ве­личинам и случайным функциям статистические характеристики несут информацию не обо всей генеральной совокупности, которая в общем случае бесконечна, а лишь о некоторой ее части — выборке, элементы которой измерены с определенными ошибками. В связи с этим в результате эксперимента получают лишь некоторые оценки параметров генеральной совокупности. Следовательно, и любая выборочная оценка — это случайная величина, точность определения которой и возможные при этом ошибки необходимо контролировать. Следует также иметь в виду, что вычисленные моменты распределения являются точечными оценками выборочных величин, так как каждый из них оценивает параметры генеральной совокупности с помощью единственного числа. Они позволяют судить о значении вычисленной статистической характеристики в данной точке и ничего не говорят о возможных пределах варьирования самой оценки.

К вычисляемым в результате эксперимента оценкам случайных величин предъявляются три основные требования: состоятельности, несмещенности и эффективности. Полагают, что оценка состоятельна, если с ростом объема выборки она стремится по вероятности к истинному значению, несмещена, если ее математическое ожидание стремится к истинному значению, и эффективна, когда оценка обладает наименьшим рассеянием по сравнению с любыми другими оценками. Из двух оценок эффективнее та, которая обладает меньшей дисперсией, т. е. значения которой рассеиваются в более узком интервале.

На уровень рассеивания оценок значительное влияние оказывают ошибки, имеющие место при эксперименте.

Как известно, при выборочном наблюдении встречаются ошибки трех видов: грубые, систематические и случайные [24]. Грубые ошибки, отличающиеся большим отклонением от центра группирования выборки, отсеиваются на этапе первичного анализа материалов.

Точность измерений любой физической величины характеризуется, как известно, абсолютной 

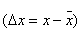
 и относительной 

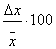
 ошибками (здесь 

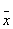
 — истинное значение), которые, в свою очередь, состоят из суммы систематических 

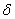
 и случайных 

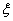
 ошибок.

Систематические ошибки

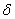
 постоянны при определении каждого члена выборки и зависят от технического уровня измерительной аппаратуры и техники эксперимента. Эти ошибки можно свести к минимуму периодической тарировкой приборов с помощью более совершенных и повышением точности метода определения исследуемых переменных.

Случайные ошибки обусловлены влиянием большого количества факторов. Их появление неодинаково и случайно от измерения к измерению и не может быть предварительно учтено из-за их зависимости от изменения условий измерений и изменчивости самих измеряемых величин. Однако при достаточно большом количестве экспериментов суммарное значение случайных ошибок, изменяющихся примерно одинаково в положительную и отрицательную сторону, приближается к нулю.

Случайные ошибки в подавляющем большинстве подчиняются нормальному закону распределения с математическим ожиданием, равным ,,0″.

В практике исследований сельскохозяйственных машин систематические и случайные ошибки близки друг к другу и совместно определяют ошибку измерений. При оценке точности измерений рекомендуется учитывать суммарную ошибку

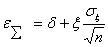
 ( 6 )

где 

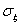
 — среднеквадратическое отклонение случайной величины 

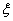
 при числе измерений n.

Для величин, определяемых косвенно — методом расчета по другим измеренным случайным величинам, оценка погрешностей осуществляется вычислением статистических оценок по соответствующим функциональным зависимостям.

Выборочные характеристики 

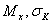
 и др., определяемые на основе ограниченного числа наблюдений, могут приближаться к истинным значениям характеристик генеральной совокупности 

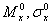
 лишь с определенной точностью e:

 ; 

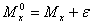
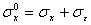
 ( 7 )

Точность выборочного наблюдения (эксперимента) может задаваться в единицах измерения исследуемой величины, в единицах выборочного значения 

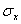
 и в процентах исследуемой величины или характеристики.

Систематическая ошибка, будучи постоянной, при этом может не учитываться.

Вероятность того, что истинное значение характеристик генеральной совокупности находится в отмеченных пределах, равна

 ; 

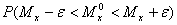
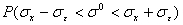
 ( 8 )

и называется надежностью данной оценки.

Так как математическое ожидание любой выборки само является случайной величиной, то полезно установить такой интервал, в котором с заданной степенью достоверности будет заключено значение оцениваемого параметра.

Интервал 

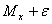
, в который в общем случае может быть произвольным 

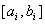
, называется доверительными границами, а соответствующая вероятность — доверительной вероятностью или, как часто говорят, надежностью. Доверительную вероятность для удобства обозначают как

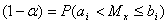
 ( 9 )

Соответственно a есть вероятность ошибки, которая на кривой распределения изображается в виде двух половинок a/2 .

Вероятность ошибки характеризует долю риска в оценке истинного значения оцениваемой величины и часто называется уровнем значимости. Для удобства величину доверительного интервала устанавливают в долях среднеквадратического отклонения 

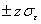
 Тогда доверительную вероятность определяют, как площадь, ограниченную кривой нормального распределения на интервале 

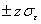
. Используя формулу стандартного нормального распределения [9]

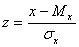
 , при M_x=0 и s_x=1, ( 10 )

доверительную вероятность, согласно ( 8 ), записывают в таком виде:

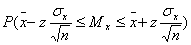
, ( 11 )

где 

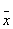
 — оценка среднего значения генеральной совокупности

Доверительный интервал для дисперсии

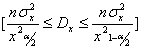
 ( 12 )

Определяют доверительный интервал в такой последовательности: вычисляют параметр выборки 

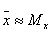
, выбирают доверительную вероятность 

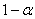
 определяют соответствующее выбранному значению 

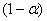
 числом из таблицы табулированных значений стандартного нормального распределения; вычисляют доверительный интервал 

.

С увеличением количества замеров достоверность эксперимента возрастает, а доверительный интервал уменьшается. Таблица используется в том случае, когда о диспер­сии исследуемой величины нельзя составить определенного мнения. Если же на основании априорных сведений или предварительных опытов 

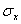
, известно, то по формуле случайной выборочной ошибки, равной половине длины доверительного интервала

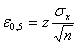
 ( 13 )

определяют необходимое число замеров, гарантирующее требуемую надежность

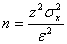
 ( 14 )

Точность и надежность оценки выборочных характеристик не следует смешивать с точностью исследования, которую часто вычисляют по такой формуле [104]:

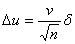
 ( 15 )

где 

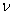
— коэффициент вариации выборочного наблюдения, % (в случае оценки точности для сельскохозяйственных машин и процессов считается достаточным, если 

%).

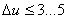
Кроме установления доверительных интервалов, задачи оценки случайных величин включают анализ законов распределения изучаемых величин, проверку принадлежности двух выборок к одной генеральной совокупности, сравнение средних дисперсий для различных выборок и др.

Рабочим инструментом статистического анализа при решении отмеченных задач оценки являются статистические гипотезы. Статистическими гипотезами именуются суждения, применяемые при различных видах анализа, касающихся, по существу, выяснения свойств некоторой генеральной совокупности случайных величин. Гипотеза в статистике трактуется как предположение о распределении случайных величин. Гипотеза, отклонения от которой приписываются данному случаю, называется нулевой и обозначается hq. Альтернативная или противоположная гипотеза называется конкурирующей и обозначается H₀.

Гипотезы проверяют при помощи специально подобранной случайной величины, распределение которой известно или может быть установлено при малом объеме выборки.

Распределение этой случайной величины принимают за распределение критерия (Сг/Мо) и обычно считают известным.

В качестве наиболее распространенных так называемых критериальных распределений применяются уже рассмотренные нами нор­мальное распределение, а также у¹-, t- и ^распределения.

Критерий Пирсона

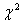
 (хи-квадрат распределение) представляет собой распределение суммы нормально распределенных случайных величин

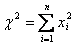
 ( 16 )

которое при п > 30 переходит в нормальное.

t-распределение Стюдента описывает распределение случайной величины

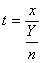
 ( 17 )

Критерий Фишера – F—распределение представляет собой распределение случайной величины

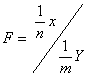
 ( 18 )

Функция того или иного критерия используется для установления доверительной границы для H₀ -гипотизы. Для проверки согласия данных с принятым законом распределения чаще используется критерий Пирсона, однако при показания по этому критерию рекомендуется доплнять другими критериями. Из них наиболее часто применяют критерии Романовского и Колмогорома-Смирнова.

Критерий Романовского вычисляют по формуле

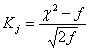
 ( 19 )

где f – число степеней свободы.

Критерий Колмогорова-Смирнова устанавливает близость теоретических и экспериментальных распределений путем сравнения их интегральных распределений и определяется по формуле

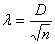
 ( 20 )

где D -максимальная граница разности накопленных теоретических m^’ и экспериментальных m частот.

В случае выборок одинакового объема для проверки гипотезы о равенстве дисперсий нескольких гауссовских случайных величин по независимым выборкам применяется критерий Кохрена, при наличии выборок различного объема – критерий Бартлетта [144]. Методика их применения приведена в специальной литературе.

Общим правило применения этих критериев является то, что, если расчетное значения каждого из них меньше табличных, то можно принять гипотезу о выбранном законе распределения.

В рассмотренных выше приемах статистической оценки характеристик генеарльной свокупности по выборочным наблюдениям каждому элементу совокупности соответствовал только один измеряемый параметр или признак, т.е. рассматривалась однофакторная система. Если исследуемая система является многомерной, применяются методы дисперсионного и регрессионного анализа. Важнейшей задачей такого анализа является выявление наличия и определения силы взаимосвязи между различными факторами. Дл этого применяются числовые характеристики: ковариацию и коэффициент корреляции. Коэффициент корреляции является безразмерной величиной (изменяемой от –1 до 1) и позволяет оценить взаимосвязь факторов, как случайных величин. В специальной литературе приводится методы его определения в конкретных ситуациях и есть стандартные программы расчета с помощью компьютерной техники. Если этот коэффициент корреляции отличен от нуля, то факторы коррелируемы. Равенство этого коэффициента нулю означает независимость факторов. Знак у коэффициента корреляции свидетельствует о отрицательном или положительном влиянии факторов. Особенности применения этого коэффициента при решении конктретных задач анализа приводятся в специальной литературе.

Одной из основных задач, которые можно решить с помощью дисперсионного анализа, является построение математических моделей, адекватно описывающих изучаемых процесс через анализ полученных результатов эсперимента или обработки данных статистических наблюдений и материалов отчетов.

Любой наблюдаемый результат из выборки N , разбитой на k уровней, можно записать как сумму математического ожидания по всей выборке m_x , значения фактора A_i на k-ом уровне и случайной ошибки ?_k в виде зависимости ? [24]

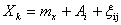
 ( 21 )

С помощью члена 

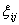
 учитываются влияния всех неконтролируемых факторов, Случайную ошибку на k-ом уровне в n-ом наблюдении обычно считают нормально распределенной с нулевым средним и постоянной дисперсией 

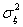
 .Для проверки значимости влияния изучаемого фактора на исследуемые параметры необходимо сравнить его дисперсию с дисперсией ошибки по F-критерию, Если окажется, что F>F_табл для выбранного уровня значимости, то изучаемый фактор значимо влияет на исследуемый параметр. Аналогичным путем проводится дисперсионный анализ для большего числа факторов. Так, для трех факторов проводится анализ модели вида [24]

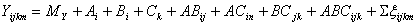
 ( 22 )

Для определения коэффициентов регрессионных моделей используются метод наименьших квадратов, метод моментов и метод максимального правдоподобия. В специальной литературе приведены соответствующие методики расчета с использованием этих методов, а также особенности их применения в конкретных ситуациях.

Адекватность модели изучаемому процессу проверяется по критерию Фишера, а значимость коэффициентов при каждом слагаемом — по критерию Стьюдента. Более подробно эти вопросы рассмотрены в специальной литературе. Используя соответствующие стандартные программы и современную компьютерную технику, можно рассчитать величину коэффициентов в моделях и дать им оценку, а также проверить адекватность модели.

При обработке большого массива данных, особенно при рассмотрении экономических проблем, нередко возникает необходимость решения задач с использованием нелинейного регрессионного анализа с учетом гетероскедастичности (непостоянством дисперсий отклонений), а также с применением методов обнаружения и оценки автокорреляции между наблюдаемыми показателями, упорядоченными во времени (временные ряды) или в пространстве (перекрестные данные) [44]. Еще одной серьезной проблемой при построении моделей множественной линейной регрессии по методу наименьших квадратов является мультиколлинеарность, т.е. линейная взаимосвязь двух или нескольких объясняющих переменных [20]. При построении регрессионных моделей иногда приходится использовать не только количественные (определяемые численно), но и фиктивные (искусственные или двоичные) переменные (индикаторы), являющиеся качественными характеристиками. Еще более сложными являются динамические модели, в которых приходится использовать не только текущие значения переменных, но и предыдущие по времени значения, т.е. с определенным запаздыванием.

В предлагаемой статье невозможно рассмотреть все варианты и особенности применения математической статистики при решении конкретных задач обработки опытных данных. Да и авторы не ставили своей задачей повторить содержание многочисленных пособий, изданных в нашей стране и за рубежом по этому вопросу. Целью этой статьи является желание обратить внимание соискателей ученых степеней, да их научных руководителей и консультантов на необходимость корректного применения математического аппарата при обработке экспериментальных данных для обоснованного формулирования научных положений, а также на необходимость владения им при публичных защитах подготовленных диссертаций. В списке литературы приведен только минимум учебной литературы, которую можно использовать для самостоятельной подготовки в данном вопросе.

---